[Java] 약수의 개수 구하기

방법1

N의 약수 개수 구하는 방법을 생각했을 때 바로 떠오르는 방법은 N을 1부터 N까지의 숫자로 나눠 약수인지 판별하여 카운트를 해주는 방법이다.

코드로 구현해보면 아래와 같다.

int N = 1000000000;

int count = 0;
for (int i = 1; i <= N; i++) {
	if (N % i == 0) count++;
}

System.out.println(count);

이 방법은 1부터 N까지 전부 검증을 해봐야하기 때문에 실행시간이 O(n)으로 N 값이 작을 땐 쓸만하지만 N 값이 커지면 아주 비효율적이다.

 

방법2

N의 약수 중 하나가 m이라고 했을 때, 다른 약수는 N/m이 되므로 하나의 약수를 알면 다른 하나의 존재가 보장이 된다.

그럼 1부터 어디까지 약수를 구해야 N의 약수의 절반을 구할 수 있을까?

아래와 그림을 참고하면 √N까지 구하면 약수 절반의 개수를 구할 수 있다는 걸 알 수 있다. (이에 대한 증명은 여기 참고)

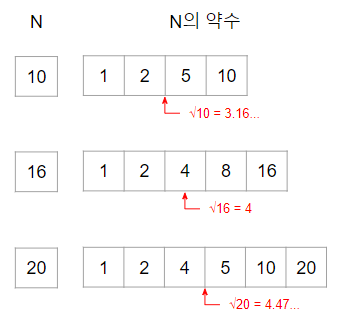
1~√N까지 수 중 N의 약수를 구해 × 2를 해주면 되고, 약수가 √N인 경우에 제곱근이므로 1개로 카운트해주면 된다.

이 내용을 코드로 작성하면 아래와 같다.

int N = 1000000000;

int count = 0;
for (int i = 1; i * i <= N; i++) {
	if (i * i == N) count++;
	else if (N % i == 0) count += 2;
}

System.out.println(count);

 

속도비교

방법2로 개선을 하면 실행시간이 O(√n)으로 단축된다.

실행시간을 비교해보면 아래와 같이 차이가 많이 나는 것을 확인해 볼 수 있다.

[방법1 실행시간]:3.63
[방법2 실행시간]:0.001